a^n:a ∈ R
n ∈ N
POTEGA(a, n)
pot = 1
for i = 1 to n
pot = pot * a
return pot
a^n:a ∈ R
n ∈ N
POTEGA(a, n)
i = n
pot = 1
pod = a
while i ≠ 0
if i MOD 2 ≠ 0
pot = pot * pod
pod = pod * pod
i = i DIV 2
return pot
a^n:a ∈ R
n ∈ N
POTEGA(a, n)
if n = 0
return 1
else
return a * POTEGA(a, n - 1)
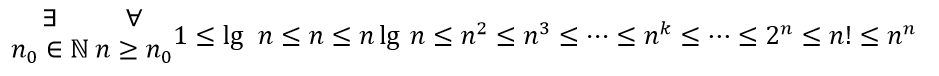
- f(n) = 13n2 + 4n - 73
- f(n) = (n2 + 1)(2n4 + 3n - 8)
- f(n) = (n3 + 3n - 1)4
- f(n) = sqrt(n + 1)
- f(n) = (n2 - 1)7
- f(n) = sqrt(n2 - 1)
- f(n) = sqrt(n2 + n)
- f(n) = (n2 + n + 1)(n3 + 5)
- f(n) = 3n
- f(n) = 2n + 1
- f(n) = 22n
- f(n) = (n + 1)2
- f(n) = (200n)2
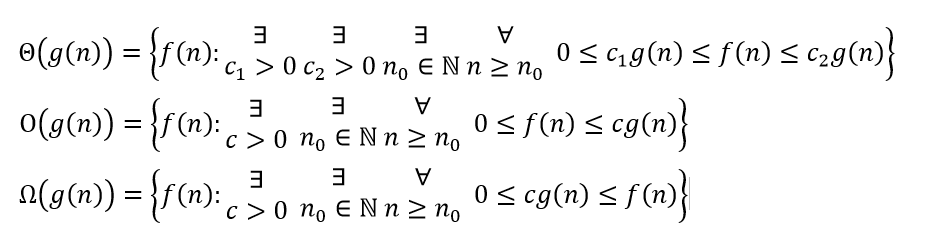
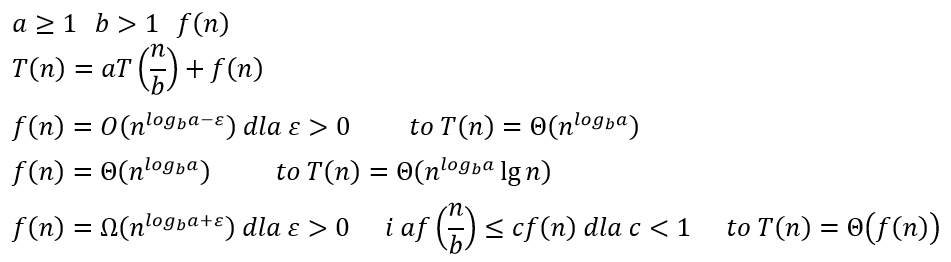
- T(n)=9T(n/3)+n
- T(n)=T(2n/3)+1
- T(n)=3T(n/4)+nlgn
- T(n)=2T(n/2)+nlgn
- T(n)=4T(n/2)+n
- T(n)=T(n-1)+1
- T(n)=4T(n/2)+n2
- T(n)=4T(n/2)+n3
- T(n)=2T(n/2)+n2
- T(n)=T(9n/10)+n
- T(n)=16T(n/4)+n2
- T(n)=7T(n/3)+n2
- T(n)=2T(n/4)+√n
- T(n)=T(n-1)+n
- T(n)=9T(n/3)+n3
- T(n)=T(n/3)+1
- T(n)=16T(n/4)+nlgn
- T(n)=2T(n/2)+5n-15
- T(n)=2T(n/3)+nlgn