a; b ∈ R
MIN(a, b)
if a < b
return a
else
return b
T
T.length ∈ N
T[i] ∈ R
x ∈ R
ZNAJDZ-ELEMENT(T, x)
i = 1
while A[i] ≠ x AND i ≠ n
i = i + 1
if A[i] ≠ x
write "nie znaleziono"
else
write i
T
T.length ∈ N
T[i] ∈ R
x ∈ R
ZNAJDZ-ELEMENT(T, x)
l = 1
p = n
repeat
s = (l + p) DIV 2
if x > A[s]
l = s + 1
else
p = s - 1
until T[s] = x OR l > p
if T[s] = x
write s
else
write "nie znaleziono"
T[n] = T[n/2] + 1
a = 1
b = 2
f(n) = 1
a^na ∈ R
n ∈ N
POTEGA(a, n)
pot = 1
for i = 1 to n
pot = pot * a
return pot
a^na ∈ R
n ∈ N
POTEGA(a, n)
i = n
pot = 1
pod = a
while i ≠ 0
if i MOD 2 ≠ 0
pot = pot * pod
pod = pod * pod
i = i DIV 2
return pot
a^na ∈ R
n ∈ N
POTEGA(a, n)
if n = 0
return 1
else
return n * POTEGA(n - 1)
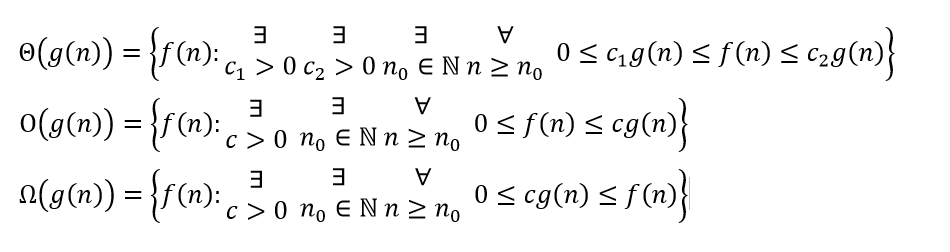

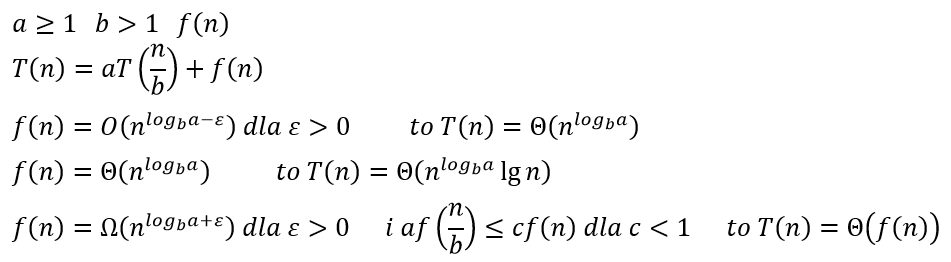
- T(n)=9T(n/3)+n
- T(n)=T(2n/3)+1
- T(n)=3T(n/4)+nlgn
- T(n)=2T(n/2)+nlgn
- T(n)=4T(n/2)+n
- T(n)=T(n-1)+1
- T(n)=4T(n/2)+n2
- T(n)=4T(n/2)+n3
- T(n)=2T(n/2)+n2
- T(n)=T(9n/10)+n
- T(n)=16T(n/4)+n2
- T(n)=7T(n/3)+n2
- T(n)=2T(n/4)+√n
- T(n)=T(n-1)+n
- T(n)=9T(n/3)+n3
- T(n)=T(n/3)+1
- T(n)=16T(n/4)+nlgn
- T(n)=2T(n/2)+5n-15
- T(n)=2T(n/3)+nlgn